Month: August 2024

Two-step equations are fundamental algebra problems requiring two operations to isolate the variable. They involve undoing addition/subtraction and multiplication/division in sequence, enhancing problem-solving skills and logical thinking. Mastering these equations builds a strong foundation for advanced math concepts and real-world applications.

What Are Two-Step Equations?

Two-step equations are algebraic expressions requiring two operations to solve for the variable. They involve a combination of addition/subtraction and multiplication/division. These equations are essential for developing problem-solving skills and logical thinking. They often appear in real-world scenarios, such as calculating distances or budgeting. Worksheets with answer keys provide structured practice, helping students master these equations and verify their solutions effectively.

Importance of Practicing Two-Step Equations

Practicing two-step equations is crucial for building foundational algebra skills. It enhances problem-solving abilities, logical thinking, and mathematical confidence. Regular practice helps students master inverse operations, ensuring accuracy in solving real-world problems. Worksheets with answer keys provide structured learning, enabling self-assessment and improvement. This practice is essential for progressing to more complex math concepts and applying mathematical reasoning in everyday scenarios effectively.

Key Concepts in Solving Two-Step Equations

Understanding inverse operations, applying them in the correct order, and maintaining balanced equations are essential skills for solving two-step equations effectively.

Understanding Inverse Operations

Inverse operations are actions that reverse each other, such as addition and subtraction or multiplication and division. Mastering these is crucial for solving two-step equations, as they help isolate the variable. For example, if an equation involves adding 5, the inverse operation would be subtracting 5. Understanding and applying these operations correctly ensures that equations remain balanced and solutions are accurate. Practice with worksheets can enhance this skill effectively.

Applying Operations in the Correct Order

Applying operations in the correct order is vital for solving two-step equations accurately. Always address addition/subtraction before multiplication/division unless parentheses dictate otherwise. This ensures equations remain balanced and variables are isolated correctly. Practicing with worksheets helps reinforce this skill, reducing errors and enhancing problem-solving efficiency. Consistent practice with such resources leads to a deeper understanding and mastery of equation-solving techniques.

Real-World Applications of Two-Step Equations

Two-step equations are essential in real-world scenarios, such as budgeting, cooking, and planning events. They help model situations like calculating total expenses or adjusting recipes. For instance, determining the cost of items after discounts or scaling ingredients proportionally. Worksheets with word problems, like earning totals or comparing quantities, make learning practical and relevant, bridging academic concepts with everyday applications.

Practice Resources for Two-Step Equations

Access free downloadable PDF worksheets with answer keys for thorough practice. These resources include problems involving integers, fractions, and decimals, along with word problems and mixed operations, suitable for various grade levels to enhance understanding and mastery of two-step equations.

Downloading Free Two-Step Equations Worksheets

Download free two-step equations worksheets in PDF format for comprehensive practice. Each worksheet includes a variety of problems, such as solving equations with integers, fractions, and decimals, as well as word problems and mixed operations. Answer keys are provided on the second page of each PDF, allowing for self-assessment and tracking progress. These resources are ideal for students in grades 6-8 to enhance their algebra skills and understanding of real-world applications. Regular practice with these worksheets ensures mastery of two-step equations and builds a strong foundation for advanced math concepts.

Using Answer Keys for Self-Assessment

Answer keys accompanying two-step equations worksheets are essential tools for self-assessment. They allow students to verify solutions, identify errors, and track progress. By comparing answers, learners can pinpoint misunderstandings and review problem-solving steps. Regular use of answer keys fosters independence, builds confidence, and ensures mastery of algebraic concepts. This approach encourages systematic learning and improves problem-solving accuracy over time.

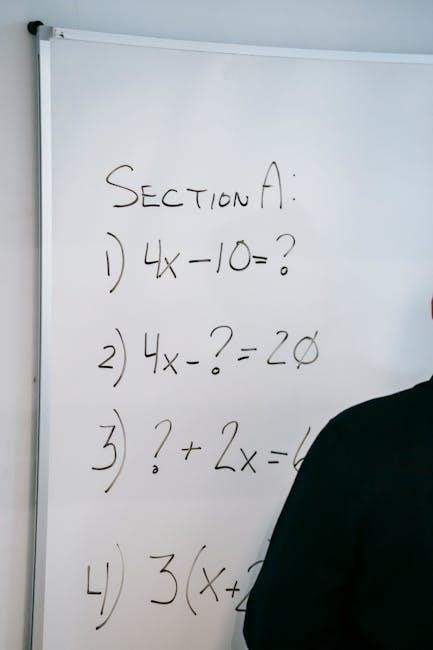
Exploring Online Tools for Additional Practice

Online platforms offer interactive tools for practicing two-step equations, providing a dynamic learning experience. Websites feature step-by-step solvers, video tutorials, and customizable worksheets. These resources allow students to explore different problem types, receive instant feedback, and track their progress; Utilizing these tools enhances engagement and understanding, making them valuable supplements to traditional practice methods for mastering two-step equations effectively.

Step-by-Step Guide to Solving Two-Step Equations

Solve two-step equations by identifying operations applied to the variable. First, undo addition or subtraction, then address multiplication or division. Use inverse operations to isolate the variable and verify the solution by substitution.

Identifying and Undoing Addition or Subtraction

To solve two-step equations, start by identifying if addition or subtraction is applied to the variable. Undo these operations first using their inverses. For example, if the equation is 3y + 6 = 12, subtract 6 from both sides to isolate the term with the variable. This step simplifies the equation, preparing it for the next operation. Always maintain balance by performing the same operation on both sides.

Undoing Multiplication or Division

After isolating the term with the variable, the next step is to undo multiplication or division. For equations like 3y ÷ 6 = 12, divide both sides by 3 to solve for y. If the equation involves multiplication, use division, and if it involves division, use multiplication. Always apply the operation to both sides to maintain balance and isolate the variable effectively. This ensures the equation remains accurate and leads to the correct solution.

Checking Solutions for Accuracy

After solving a two-step equation, substitute the solution back into the original equation to verify correctness. For example, if x = 4 is the solution, replace x in the equation and check if both sides are equal. This step ensures the solution is valid and reinforces understanding of inverse operations, providing confidence in the problem-solving process and maintaining accuracy in mathematical outcomes.

Common Mistakes and Tips for Success

Common mistakes include incorrect operation order and miscalculations. Tips for success involve using inverse operations properly and ensuring equations remain balanced throughout the solving process.

Avoiding Errors in Inverse Operations

Avoiding errors in inverse operations requires careful attention to the order of operations. Always undo addition or subtraction before addressing multiplication or division. For example, in the equation 3y + 6 = 12, subtract 6 from both sides first, then divide by 3 to find y = 2. This systematic approach ensures accuracy and prevents common mistakes. Regular practice with worksheets helps build proficiency in applying inverse operations correctly.

Keeping Equations Balanced

Keeping equations balanced is crucial for accurate solutions. When performing operations, ensure the same action is applied to both sides. For example, if subtracting 5 from one side, subtract 5 from the other. This maintains equality and prevents errors. Always write down each step clearly, using inverse operations correctly to isolate the variable. This disciplined approach ensures the equation remains balanced throughout the solving process, leading to correct solutions every time.

Organizing Work for Clarity

Organizing your work is essential for solving two-step equations effectively. Write down each step clearly, showing how you undo operations to isolate the variable. Use inverse operations in the correct order, ensuring each action is visible. This clarity helps in understanding the problem and reduces errors. Properly formatting your work also makes it easier to review and verify solutions, ensuring accuracy and confidence in your answers.

Advanced Problems and Word Scenarios

Advanced two-step equations involve fractions, decimals, and word problems, challenging students to apply their skills in real-world contexts for a more comprehensive understanding of algebraic concepts.

Solving Two-Step Equations with Fractions and Decimals

To solve two-step equations involving fractions and decimals, first isolate the term with the variable using inverse operations. For fractions, multiply or divide by their reciprocals, and for decimals, convert them to whole numbers by multiplying or dividing. Always check your solution by substituting it back into the original equation to ensure accuracy and understanding.

Translating Word Problems into Equations

Translating word problems into equations involves identifying key terms and converting them into mathematical expressions. Understand the relationships described, such as “total,” “less than,” or “five times,” and represent them using variables and operations. Practice with real-world scenarios, like calculating earnings or quantities, to enhance your ability to form accurate two-step equations and solve them effectively for various applications.

Practicing with Mixed Operation Problems

Mixed operation problems combine addition, subtraction, multiplication, and division, requiring a systematic approach. Start by simplifying the equation step-by-step, ensuring the correct order of operations. These problems enhance critical thinking and problem-solving skills, preparing students for more complex algebraic challenges. Regular practice with mixed operations strengthens mathematical fluency and accuracy in solving two-step equations.

Evaluating Mastery and Progress

Evaluate understanding by using worksheets to assess problem-solving skills. Track improvement over time through consistent practice and review. Use answer keys to identify strengths and areas needing refinement.

Using Worksheets to Assess Understanding

Worksheets are an effective tool for assessing mastery of two-step equations. They provide a structured format to practice and evaluate problem-solving skills, covering integers, fractions, and decimals. Each worksheet includes a variety of problems, allowing students to demonstrate their understanding of inverse operations and algebraic concepts. Answer keys enable immediate feedback, helping identify areas where additional practice is needed.

Regular use of worksheets ensures progress tracking and reinforces learning. They are ideal for self-assessment or classroom use, offering a clear measure of comprehension and readiness for more complex math topics.

Tracking Improvement Over Time

Regularly using two-step equations worksheets allows students to track their progress effectively. By completing worksheets over time, learners can identify areas of improvement and monitor their mastery of algebraic concepts. Answer keys provide immediate feedback, enabling students to correct mistakes and build confidence. Consistent practice with varied problems involving integers, fractions, and decimals ensures steady growth and improved problem-solving skills in math.

Seeking Feedback from Teachers or Peers

Engaging with teachers or peers enhances learning by providing constructive feedback on two-step equations. Discussing solutions and strategies clarifies doubts and refines problem-solving techniques. Collaborative review of worksheets and answers fosters understanding and identifies areas needing attention. This interaction supports personalized growth and reinforces algebraic principles effectively.

Additional Resources for Learning

Explore free two-step equations worksheets with answer keys from Kuta Software and WorksheetWorks. These PDF resources include practice problems with integers, fractions, and decimals for all skill levels.

Recommended Websites for Interactive Practice

Visit Kuta Software and WorksheetWorks for interactive two-step equations practice. These websites offer customizable worksheets, answer keys, and step-by-step solutions; They provide problems with integers, fractions, and decimals, as well as word problems, ideal for 6th to 8th-grade students. Their interactive tools allow real-time problem solving, making learning engaging and effective for mastering algebraic concepts.

Video Tutorials for Visual Learners

YouTube channels like Khan Academy and Math Antics offer excellent video tutorials for solving two-step equations. These visual guides provide step-by-step explanations, making complex concepts easier to grasp. They often include examples with fractions, decimals, and word problems, allowing learners to see the process in action. Visual learners can benefit from pausing, replaying, and following along with the tutorials to enhance their understanding and retention of algebraic principles.

Study Guides and Reference Materials

Study guides and reference materials provide comprehensive support for mastering two-step equations. Websites like Khan Academy and MathWorks offer detailed step-by-step examples and practice exercises. These resources often include interactive activities, printable worksheets, and solutions to common problems. They cater to different learning styles, ensuring students can review concepts, practice independently, and reinforce their understanding of algebraic principles at their own pace.

Mastering two-step equations is achievable with consistent practice. Utilize worksheets and answer keys to reinforce skills, ensuring accuracy and confidence in solving algebraic problems effectively over time.

Summarizing Key Takeaways

Two-step equations require undoing operations in sequence, starting with addition/subtraction and then multiplication/division. Practice with worksheets and answer keys enhances problem-solving skills and accuracy. These resources, available as PDFs, include problems involving integers, fractions, and decimals, helping students apply algebraic concepts to real-world scenarios. Regular practice builds confidence and mastery, ensuring a strong foundation for advanced math topics.

Encouraging Continued Practice

Consistent practice is key to mastering two-step equations. Utilize free PDF worksheets and answer keys to reinforce skills and build confidence. These resources offer varied problems, including integers, fractions, and decimals, ensuring comprehensive understanding. Encourage students to solve a few problems daily, applying algebraic concepts to real-world scenarios. Regular practice fosters problem-solving abilities and prepares learners for advanced math challenges. Parents and educators can motivate students by celebrating progress and providing support.

Final Thoughts on Mastering Two-Step Equations

Mastery of two-step equations is achievable through dedicated practice and understanding of inverse operations. Free PDF worksheets with answer keys provide excellent tools for honing skills. Emphasize the importance of showing work and checking solutions for accuracy. Encourage learners to apply these concepts to real-world problems, reinforcing their practical value. With persistence and the right resources, students can confidently solve two-step equations and excel in algebra.

Step into the magical world of Harry Potter Coloring Pages PDF, offering a collection of enchanting designs featuring beloved characters, iconic scenes, and spellbinding details for all ages.

1.1. Overview of Harry Potter Coloring Pages

Harry Potter coloring pages offer a variety of magical designs, featuring iconic characters like Harry, Hermione, and Ron, along with enchanting scenes from Hogwarts. These pages are perfect for fans of all ages, combining creativity with a love for the wizarding world, available in convenient PDF formats for easy printing.

1.2. Importance of PDF Format for Coloring Pages

The PDF format ensures high-quality, printable designs for Harry Potter coloring pages, maintaining clarity and detail. It allows easy downloading and sharing, making it accessible for fans worldwide. PDFs are ideal for preserving the integrity of intricate illustrations, ensuring a seamless coloring experience for both children and adults.

Benefits of Harry Potter Coloring Pages

Harry Potter coloring pages offer a creative outlet, fostering imagination and relaxation. They are perfect for all ages, providing a fun way to engage with the wizarding world while promoting mindfulness and artistic expression.

2.1. Educational and Creative Development for Children

Harry Potter coloring pages PDFs are a fantastic tool for children, enhancing fine motor skills and creativity. They inspire imaginative storytelling and problem-solving, while vibrant themes spark curiosity and learning. These pages also encourage focus and self-expression, making them a fun and educational activity for young minds.

2.2. Stress Relief and Relaxation for Adults

Engaging with Harry Potter coloring pages offers adults a therapeutic escape, promoting mindfulness and relaxation. The repetitive motion of coloring combined with the magical themes creates a calming experience, helping to reduce stress and anxiety. Perfect for unwinding, these pages allow adults to reconnect with their creative side and enjoy a peaceful, meditative activity.

2;3. Enhancing Fine Motor Skills and Focus

Coloring Harry Potter pages helps refine fine motor skills, as intricate designs require precision and control. This activity also sharpens focus and concentration, encouraging patience and attention to detail. Ideal for both children and adults, it fosters creativity while improving dexterity and hand-eye coordination.

Popular Sources for Harry Potter Coloring Pages PDF

Discover a variety of sources offering Harry Potter Coloring Pages PDF, including official websites, fan communities, and online platforms providing free and premium downloads for fans of all ages.

3.1. Official Harry Potter Websites and Merchandise

Official Harry Potter websites and merchandise stores offer exclusive coloring pages PDF featuring authentic characters, scenes, and artwork. These high-quality downloads are designed for fans of all ages, providing a magical way to engage with the wizarding world through creative coloring experiences.

3.2. Fan-Made Art and Community Contributions

Discover the creativity of the Harry Potter fan community through unique, fan-made art and designs. These coloring pages PDF often feature original interpretations of characters, scenes, and magical creatures, offering a diverse and imaginative take on the wizarding world. Fans share their passion by creating and distributing these free, high-quality downloads.

3.3. Free vs. Premium Coloring Page Websites

Explore the difference between free and premium Harry Potter coloring pages PDF. Free options offer a variety of designs for casual fans, while premium sites provide exclusive, high-quality, and intricate artwork. Premium downloads often include bonus content, making them a great choice for enthusiasts seeking unique and detailed coloring experiences.

Popular Characters Featured in Coloring Pages

Harry Potter coloring pages PDF highlight iconic characters like Harry, Hermione, Ron, Dumbledore, and Voldemort, offering a diverse range of magical figures for fans to color and enjoy creatively.

4.1. Harry Potter, Hermione Granger, and Ron Weasley

The trio of Harry Potter, Hermione Granger, and Ron Weasley are central to the coloring pages, showcasing their friendship and adventures. These designs often feature them in iconic Hogwarts settings, battling dark forces, or solving magical mysteries, making them a favorite among fans of all ages to color and personalize.

4.2. Iconic Villains: Lord Voldemort and His Followers

Lord Voldemort and his devoted followers, including Bellatrix Lestrange and Lucius Malfoy, are prominently featured in these coloring pages. Their intimidating presence and dark themes captivate fans, offering a dramatic contrast to the heroic trio. These designs often depict intense battle scenes, allowing enthusiasts to creatively express the sinister side of the wizarding world.

4.3. Beloved Professors: Dumbledore, Snape, and More

Coloring pages often feature Dumbledore, Snape, and other professors, showcasing their wisdom, complexity, and unique personalities. These designs highlight their iconic roles, from Dumbledore’s gentle guidance to Snape’s mysterious intensity. They also include other beloved educators like McGonagall and Professor Sprout, bringing Hogwarts’ academic magic to life for fans of all ages.

Therapeutic Benefits of Coloring

Engaging with Harry Potter coloring pages fosters mindfulness, reduces stress, and enhances mental clarity. This calming activity promotes emotional well-being for both adults and children, offering a creative escape into Hogwarts’ magical world.

5.1. Mindfulness and Stress Reduction

Coloring Harry Potter PDF pages promotes mindfulness by focusing on intricate designs and beloved characters. This meditative process distracts from daily stress, offering a calming escape into a magical world, fostering relaxation and emotional balance for both children and adults alike.

5.2. Enhancing Creativity and Self-Expression

Coloring Harry Potter PDF pages sparks creativity, allowing users to bring magical characters and scenes to life with vibrant colors. This activity encourages personal expression, inspiring imagination and artistic freedom while exploring the wizarding world, making it a delightful outlet for both children and adults to showcase their unique styles.

5.3. Improving Concentration and Mental Clarity

Engaging with Harry Potter coloring pages PDF fosters mindfulness, helping users focus on intricate details and calming their minds. The repetitive, meditative motion of coloring enhances concentration and mental clarity, offering a therapeutic escape and a sense of accomplishment in bringing the wizarding world to vibrant life.

Tips and Techniques for Coloring Harry Potter Pages

Enhance your coloring experience with quality tools like colored pencils or markers. Experiment with layering colors for depth and use shading techniques to bring magical details to life.

6.1. Choosing the Right Coloring Tools

Selecting the right tools is essential for a magical coloring experience. Opt for high-quality colored pencils, markers, or crayons for vibrant results. Consider digital tools for precision or traditional media for a tactile feel. Pair your tools with smooth, heavy-duty paper to ensure colors pop and details stay crisp.

6.2. Layering Colors for Depth and Dimension

Layering colors adds depth and dimension to your Harry Potter coloring pages. Start with light base tones, then gradually build up darker shades to create intricate details. Experiment with blending techniques to achieve smooth transitions, making magical scenes like Hogwarts castles or Quidditch matches truly stand out with a professional finish.

6.3. Shading Techniques to Enhance Details

Shading techniques can elevate your Harry Potter coloring pages by adding complexity and realism. Use gradients and shadows to highlight magical creatures, Hogwarts architecture, or character expressions. Start with light strokes, then deepen tones for dimension. This method enhances intricate details, bringing the wizarding world to life with precision and artistic flair.

User Testimonials and Reviews

Users praise the Harry Potter coloring pages for being free, educational, and fun, perfect for fans of all ages to enjoy and create magically.

7.1. Feedback from Parents and Educators

Parents and educators rave about Harry Potter coloring pages for their educational value, fostering creativity and calmness in children. Many appreciate the free PDF accessibility, making it easy to print and use in classrooms or at home, while also serving as a stress-relief activity for adults.

7.2. Experiences of Adult Coloring Enthusiasts

Adult coloring enthusiasts often praise Harry Potter coloring pages for their therapeutic benefits and nostalgic appeal. These PDF printables provide a creative outlet, allowing adults to unwind and express their artistic side while reconnecting with the magical world of Hogwarts and its beloved characters.

7.3. Opinions from Die-Hard Harry Potter Fans

Die-hard Harry Potter fans enthusiastically embrace these coloring pages as a fun way to engage with the series. The PDF format offers easy access to a wide variety of characters and scenes, allowing fans to express their creativity while connecting with the magical world they love and cherish deeply.

Seasonal and Event-Based Coloring Pages

Celebrate magical moments with Harry Potter coloring pages designed for holidays like Halloween and Christmas, or special editions marking movie anniversaries and other events.

8.1. Halloween Themes with Dementors and Ghosts

Discover spooky Halloween-themed Harry Potter coloring pages, featuring eerie Dementors, ghostly figures, and haunted scenes from the wizarding world. These magical designs bring a touch of mystery and excitement to your festive coloring sessions, perfect for fans of all ages to enjoy during the Halloween season.

8.2. Christmas and Holiday-Themed Pages

Celebrate the festive season with Christmas and holiday-themed Harry Potter coloring pages, showcasing Hogwarts adorned with twinkling lights, snow-covered landscapes, and beloved characters in festive attire. These magical designs bring the wizarding world to life during the holidays, offering a fun and creative way to embrace the season.

8.3. Special Editions for Movie Anniversaries

Commemorate the magic of Harry Potter with special edition coloring pages released for movie anniversaries. These unique designs feature iconic scenes and beloved characters, offering exclusive artwork. Perfect for collectors and fans, they bring nostalgia and creativity together, celebrating the wizarding world’s cinematic legacy and enchanting new generations.

Harry Potter Coloring Page Contests and Communities

Join vibrant communities and contests celebrating Harry Potter coloring pages. Participate in challenges, win prizes, and connect with fellow fans, fostering creativity and camaraderie worldwide.

9.1. Online Coloring Competitions and Prizes

Engage in online coloring competitions featuring Harry Potter themes, where participants can showcase their creativity and win exciting prizes. These contests often involve submitting colored pages, with winners selected based on creativity, detail, and adherence to the magical world’s essence, fostering a sense of achievement and community among enthusiasts.

9.2. Social Media Groups and Sharing Platforms

Join vibrant social media groups dedicated to Harry Potter coloring pages, where fans share their creations, gain inspiration, and receive feedback. Platforms like Facebook and Instagram host communities that celebrate artistic interpretations of the wizarding world, fostering connections among enthusiasts and encouraging creativity globally.

9.3. Collaborative Projects and Fan Art Initiatives

Engage in collaborative projects where fans collectively create large-scale fan art using Harry Potter coloring pages. These initiatives often result in stunning themed books or exhibitions, fostering creativity and a sense of community. Participants can share their interpretations, sparking inspiration and showcasing the magical world’s enduring appeal for both kids and adults alike.

Cultural Impact of Harry Potter Coloring Pages

Harry Potter coloring pages have become a cultural phenomenon, inspiring fan art, fostering creativity, and uniting fans worldwide. Their popularity has helped popularize adult coloring trends and celebrate the wizarding world’s timeless magic.

10.1. Role in Popularizing Adult Coloring Trends

Harry Potter coloring pages have significantly contributed to the rise of adult coloring, offering a therapeutic outlet and fostering creativity. Their detailed, magical designs appeal to adults, making them a key part of the trend’s growth and popularity worldwide.

10.2. Influence on Fan Art and Creative Expression

Harry Potter coloring pages have inspired a wave of fan art, allowing enthusiasts to express their creativity. These PDFs provide a canvas for fans to bring characters to life, blending official designs with personal artistic styles, fostering creativity and inspiring new interpretations of the beloved wizarding world.

10.3. Bridging Generations Through Shared Interests

Harry Potter coloring pages PDFs unite generations, offering a shared creative outlet for fans of all ages. Whether it’s a child, parent, or grandparent, these magical designs inspire collaborative art-making, fostering mutual enjoyment and a deeper connection to the wizarding world, creating lasting memories together.

Harry Potter coloring pages PDF offer a magical, creative outlet for fans of all ages. Whether for relaxation, learning, or fun, these pages bring the wizarding world to life, inspiring imagination and joy in everyone who colors them.

11.1. Summary of Key Points

Harry Potter Coloring Pages PDF offer a magical, creative outlet for fans of all ages. Featuring beloved characters, iconic scenes, and detailed designs, these pages provide relaxation, learning, and fun. They inspire imagination, foster creativity, and bring the wizarding world to life, making them a delightful activity for everyone.

11.2. Encouragement to Try Harry Potter Coloring Pages

Embark on a magical adventure with Harry Potter Coloring Pages PDF! These free, printable sheets bring Hogwarts to life, offering fun for kids and adults alike. Perfect for relaxing, expressing creativity, and enjoying the wizarding world, they’re a must-try for every Harry Potter fan.

11.3. Final Tips for Making the Most of the Experience

Experiment with colors, try layering techniques, and use quality tools for vibrant results. Discover the magical world of Harry Potter through these printable sheets. Take breaks, stay relaxed, and share your creations with fellow fans to enhance your enjoyment and make the experience truly fulfilling and memorable for all ages.

Welcome to the comprehensive guide for your air fryer! This manual provides essential information for safe usage, understanding components, and optimizing your cooking experience with step-by-step instructions.

Overview of the Air Fryer and Its Benefits

The air fryer is a revolutionary kitchen appliance that uses rapid air technology to cook food with minimal oil, offering a healthier alternative to deep-frying. It operates by circulating hot air around food, achieving crispy results with up to 90% less fat. This versatile appliance allows users to fry, roast, grill, and bake various dishes effortlessly. Its compact design and energy efficiency make it a practical addition to modern kitchens. The air fryer is ideal for preparing snacks, main courses, and desserts, catering to diverse dietary needs. Its ease of use and cleanup further enhance its appeal, making it a must-have for home cooks and health-conscious individuals alike.

Importance of Reading the Manual Before Use

Reading the air fryer manual is crucial for safe and effective operation. It provides essential safety precautions, such as avoiding water contact and ensuring the basket is fully closed during use. Understanding the appliance’s components and controls helps prevent accidents and optimizes performance. The manual also outlines proper food preparation techniques and recommends cooking times and temperatures for various dishes. Familiarizing yourself with troubleshooting tips ensures you can address common issues quickly. By following the guidelines, you can enjoy a seamless cooking experience while maintaining the longevity of your air fryer. Always refer to the manual for specific instructions tailored to your model.

Key Components and Accessories

This section introduces the essential parts and additional items included with your air fryer, ensuring a comprehensive understanding of its design and functionality for optimal use.

Understanding the Air Fryer Parts and Functions

The air fryer consists of key components like the frying basket, pan, and air inlet, designed for efficient hot air circulation. The basket holds food, while the pan collects excess oil. The air inlet ensures proper airflow for even cooking. Digital controls or buttons allow easy temperature and time adjustments. Understanding these parts is crucial for safe and effective operation. Always ensure the basket is fully closed during use to avoid malfunctions. Regular cleaning of these components maintains hygiene and performance. Refer to the manual for detailed diagrams and care instructions to maximize your air fryer’s longevity and functionality.

Accessories Included with the Air Fryer

Your air fryer typically comes with essential accessories like the frying basket and pan, designed for easy food preparation and cleanup. Some models include additional items such as non-stick liners, tongs, or recipe books. The frying basket is perforated to ensure air circulation, while the pan collects excess oil. Optional accessories like grill plates or dividers may be available for versatile cooking. Always refer to the manual for specific details on included items and their usage. These accessories enhance your cooking experience and help maintain the air fryer’s performance; Ensure all parts are cleaned regularly for optimal functionality and longevity.

Safety Precautions and Warnings

Always follow safety guidelines to avoid accidents. Keep children away, avoid overheating, and ensure the air fryer is placed on a stable, heat-resistant surface. Never submerge electrical parts in water.

General Safety Guidelines for Operating the Air Fryer

Ensure the air fryer is placed on a stable, heat-resistant surface away from flammable materials. Always keep children away and avoid touching hot surfaces during operation. Never submerge electrical components in water or operate the air fryer near water sources. Avoid overheating by not leaving the appliance unattended. Use oven mitts or tongs to handle the basket and drawer. Do not cook extremely greasy foods like sausages, as they may cause splatter.
Regularly clean the air fryer to prevent food residue buildup. Always turn off and unplug the device before cleaning or maintenance. Follow these guidelines to ensure safe and effective use of your air fryer;

Electrical Safety and Handling Precautions

Never submerge the air fryer or its electrical components in water, as this can cause severe damage or electrical shock. Avoid operating the appliance near water sources or in humid environments. Do not handle the air fryer with wet hands or while standing on a damp surface. Ensure the power cord is kept away from heat sources and avoid overstretching or pinching it. Use the air fryer only with the voltage specified in the manual. Never use multiple plug adapters or extension cords, as this may lead to electrical hazards. Always unplug the appliance when not in use or during cleaning to ensure safety.

Operating the Air Fryer

Plug in the air fryer, place food in the basket, set temperature and timer via controls, and press start for efficient cooking.

Preparing the Air Fryer for First Use

Before using your air fryer for the first time, ensure all components are unpacked and inspected for damage. Wash the basket, pan, and accessories with warm soapy water, then dry thoroughly. Place the air fryer on a stable, heat-resistant surface. Plug in the device, ensuring the power cord is securely connected. Preheat the air fryer at 400°F (200°C) for 5-10 minutes to eliminate any manufacturing smells. Always follow the manufacturer’s guidelines to ensure proper preparation and safety.

Basic Cooking Instructions and Controls

Start by placing your food in the air fryer basket, ensuring it is evenly spread for optimal cooking. Set the timer and temperature using the control panel—typically, temperatures range from 175°F to 400°F (80°C to 200°C). Press the START button to begin cooking. For best results, pat dry foods like fries or chicken to enhance crispiness. Avoid overcrowding the basket, as this can affect air circulation. Shake the basket midway through cooking for even results; Always use oven mitts or tongs when handling hot food. Refer to the manual for specific cooking times and temperatures for various foods. Ensure the air fryer is turned off before removing the drawer or basket.

Navigating the Digital Interface (if applicable)

Modern air fryers often feature a digital interface for precise control. Use the touchscreen or buttons to select preset programs for common dishes like fries or chicken. Adjust cooking time and temperature by navigating through the menu. Press the START button to begin. Some models allow custom settings for tailored results. Use the +/- buttons to fine-tune values. Ensure the display shows your desired settings before starting. For advanced features, refer to the manual for guidance on functions like dehydration or slow cooking. Always confirm selections before initiating the cooking cycle for optimal performance and safety. This interface simplifies achieving perfect results every time.

Cooking Tips and Best Practices

Pat food dry before cooking for crispy results. Use minimal oil for healthier meals. Avoid overcrowding the basket for even cooking. Preheat the air fryer for optimal performance and consistent results. Shake or flip food halfway through cooking for uniform browning. Experiment with marinades and seasonings for enhanced flavor. Adjust cooking time and temperature based on food type and desired crispiness. Regularly clean the air fryer to maintain efficiency and hygiene. Follow recommended portion sizes for best outcomes. These tips ensure delicious, evenly cooked dishes every time, making your air fryer experience enjoyable and rewarding. Always refer to the manual for specific guidelines.

Optimizing Food Preparation and Results

To achieve the best results with your air fryer, ensure food is evenly distributed in the basket to allow proper air circulation. Pat dry foods like meat or vegetables before cooking to enhance crispiness. Lightly brush food with oil or seasonings for flavor, but avoid overloading, as this can hinder performance. Preheating the air fryer for a few minutes before cooking helps maintain consistent temperatures. For delicate foods, use lower heat settings, while higher temperatures work well for crisping. Shake the basket halfway through cooking to ensure even browning. Marinate or season foods beforehand for added flavor. Cleaning the air fryer regularly ensures optimal airflow and prevents residue buildup. Always refer to the manual for specific food type guidelines to achieve perfect results every time.

Common Recipes and Cooking Times

Popular air fryer recipes include crispy fries (15-20 minutes at 180°C), chicken wings (20-25 minutes at 200°C), and steak (10-15 minutes at 220°C). Vegetables like broccoli or cauliflower cook in 10-12 minutes at 180°C. Shrimp takes 8-10 minutes at 200°C. Frozen foods such as nuggets or fries require 10-15 minutes at 180-200°C. Ensure food is evenly spread and shaken halfway for uniform cooking. Adjust times based on portion size and desired crispiness. Always preheat for 2-3 minutes before cooking. These times are approximate and may vary depending on your air fryer model. Refer to the manual for specific guidelines.

Maintenance and Cleaning

Regularly clean the air fryer after each use by washing the basket and pan with mild soap and warm water. Avoid using abrasive cleaners or metal scourers.

Regular Cleaning Procedures for the Air Fryer

Regular cleaning is essential for maintaining your air fryer’s performance and hygiene. After each use, wash the basket and pan with mild soap and warm water. Avoid using abrasive cleaners or metal scourers, as they may damage the non-stick coating. For tough food residue, soak the parts in warm soapy water for 30 minutes before scrubbing gently. Dry all components thoroughly to prevent rust or water spots. Clean the exterior with a damp cloth, avoiding electrical components. Regular cleaning ensures optimal airflow and prevents food odors from lingering. Always allow the air fryer to cool completely before cleaning to avoid burns or damage.

Storage and Longevity Tips

To ensure your air fryer lasts long, store it in a cool, dry place away from direct sunlight. After cleaning and drying, place the basket and pan inside the main unit. Avoid stacking heavy objects on top of the air fryer to prevent damage. Store accessories separately to maintain their shape and functionality. For extended storage, ensure all parts are completely dry to prevent moisture buildup. Regular maintenance and proper storage will help preserve the air fryer’s performance and extend its lifespan. Always refer to the manual for specific storage recommendations to keep your appliance in optimal condition.

Troubleshooting Common Issues

Address common issues like the air fryer not turning on, uneven cooking, or basket fitting problems. Ensure the basket is fully closed and check power connections. Avoid overloading, clean regularly, and refer to the manual for specific solutions to maintain optimal performance.

Resolving Errors and Malfunctions

If your air fryer malfunctions, start by checking power connections and ensuring the basket is fully closed. For error codes, consult the manual for specific solutions. Regular cleaning prevents issues like food residue buildup. If the air fryer overheats, unplug it and let it cool. Resetting the device may resolve digital interface glitches. Always refer to the troubleshooting section for detailed guidance. Follow safety guidelines and contact customer support if problems persist. Proper maintenance and adherence to instructions can prevent most malfunctions, ensuring safe and efficient cooking experiences.

Addressing Frequently Asked Questions

Common questions about air fryer usage include optimal cooking times, food preparation tips, and troubleshooting. Users often ask why food isn’t crispy—usually due to overcrowding or insufficient pat-drying. For sticky food, lightly spray the basket. Cleaning is another concern; soak parts in warm water and avoid harsh chemicals. Many wonder about suitable foods; most can be cooked, but avoid wet batters. For error codes, reset the device or check connections. Always ensure the basket is fully closed. These FAQs ensure smooth operation and enhance your cooking experience. Refer to specific sections for detailed solutions and tips.

Overview of the Honeywell RTH221B1021 Thermostat

The Honeywell RTH221B1021 is a programmable thermostat with an LCD display, offering a 1-week schedule and 4 time periods per day. It features intuitive controls, compatibility with various heating and cooling systems, and energy-efficient settings, making it a practical solution for precise temperature management in homes and offices.

1.1 Key Features and Benefits

The Honeywell RTH221B1021 features a backlit LCD display for easy temperature control, 1-week programmable scheduling, and 4 time periods per day. It offers precise temperature accuracy, energy-saving modes, and compatibility with most heating and cooling systems. The thermostat is user-friendly, with intuitive controls and a compact design. It supports smart response technology for efficient temperature regulation and includes options for customizing system settings to optimize comfort and energy savings.

1.2 Compatibility and Installation Requirements

The Honeywell RTH221B1021 is compatible with most heating and cooling systems, including gas, electric, and heat pumps. Installation requires basic wiring knowledge and tools. Ensure your system matches the terminal designations (e.g., R, W, Y, G, C). If replacing an old thermostat, label wires carefully for proper connection. Battery-powered, it eliminates the need for a common wire. Suitable for single-stage systems, it supports 4 periods per day. Follow manual instructions for mercury disposal if upgrading from an older model.

Installation and Setup Guide

The Honeywell RTH221B1021 installation involves removing the old thermostat, labeling wires, and mounting the new device. Ensure proper terminal designation and follow disposal instructions for mercury thermostats.

2.1 Removing the Old Thermostat

To remove the old thermostat, first switch off the HVAC system and ensure the power is disconnected. Gently pull the thermostat away from the wall to access the wires. Label each wire with its terminal designation for easy identification during installation. If the old thermostat contains mercury, handle it carefully and refer to the disposal instructions provided in the manual. Store the old unit securely to prevent damage.

2.2 Labeling Wires and Terminal Designation

Labeling wires is crucial for a smooth installation. Use the provided labels or create new ones to mark each wire according to its terminal designation (e.g., R, W, Y, G, C). Refer to the manual for terminal mapping. Ensure wires are securely attached to their respective terminals. Double-check connections before proceeding to avoid system malfunctions. Proper labeling ensures accurate wiring, simplifying the installation process and preventing errors. This step is essential for safe and efficient thermostat operation.

2.3 Mounting the New Thermostat

Mounting the Honeywell RTH221B1021 thermostat involves securing it to the wall using the provided mounting screws. Ensure the device is level and properly aligned for accurate temperature readings. Connect the labeled wires to the corresponding terminals, double-checking for correct terminal designation. Once wired, attach the thermostat faceplate securely to the wall plate. Turn the power back on and verify the LCD display lights up, confirming successful installation. This step ensures the thermostat operates efficiently and maintains precise temperature control.

Programming the Thermostat

The Honeywell RTH221B1021 features an LCD display and intuitive controls for setting daily schedules and temperature adjustments. It allows users to program up to four time periods per day, ensuring efficient temperature management.

3.1 Understanding the LCD Display

The Honeywell RTH221B1021 features a clear LCD display that shows current temperature, set temperature, system status, and time. The display is backlit for easy viewing in low-light conditions. Icons indicate heating, cooling, or fan operation, while arrows show temperature adjustments. The “NEXT” and “DONE” buttons help navigate settings. The display also highlights energy-saving modes and schedule status, ensuring users can monitor and control their settings efficiently. This intuitive interface simplifies programming and daily use.

3.2 Setting Up Daily Schedules

Setting up daily schedules on the Honeywell RTH221B1021 is straightforward. Press the “Menu” button and navigate to the schedule setup option. Choose your preferred schedule type, such as 4 periods per day, and set the time and temperature for each period. Use the up/down arrows to adjust settings, and press “Done” to save. The thermostat allows for flexible programming, ensuring consistent comfort while optimizing energy use. Regularly review and adjust schedules to match lifestyle changes or seasonal needs.

3.3 Adjusting Temperature Settings

The Honeywell RTH221B1021 allows users to adjust temperature settings with ease. Use the up and down arrows to increase or decrease the setpoint. The thermostat offers precise temperature control, with an accuracy of ±1 degree. Users can manually set the desired temperature or program scheduled settings. The LCD display clearly shows the current and set temperatures. Adjustments can be made in 1-degree increments for optimal comfort.

Advanced Features and Settings

The Honeywell RTH221B1021 offers advanced features such as energy-saving modes, Smart Response Technology, and customizable system settings to enhance efficiency and user experience for optimal performance.

4.1 Energy-Saving Modes

The Honeywell RTH221B1021 features energy-saving modes designed to optimize heating and cooling usage. These modes help reduce energy consumption by automatically adjusting temperatures during off-peak hours. The thermostat also offers smart response technology, which learns your system’s operation to maintain efficiency. Additionally, its programmable scheduling allows you to set energy-saving preferences, ensuring comfort while lowering utility bills. These modes are ideal for eco-conscious users seeking to balance energy efficiency with consistent home comfort.

4.2 Smart Response Technology

The Honeywell RTH221B1021 features Smart Response Technology, which optimizes temperature control by learning your system’s behavior. It adjusts heating and cooling cycles to maintain consistent comfort while reducing energy use. This advanced feature ensures precise temperature management, adapting to your home’s unique conditions for enhanced efficiency and reliability.

4.4 Customizing System Settings

The Honeywell RTH221B1021 allows users to customize system settings for enhanced comfort and efficiency. Adjustments include modifying temperature ranges, enabling energy-saving modes, and setting custom schedules. Users can also fine-tune temperature accuracy and customize display settings like brightness and units. Additionally, features such as keypad lock and Smart Response Technology can be personalized to suit individual preferences, ensuring optimal performance tailored to specific HVAC systems and lifestyles.

Troubleshooting Common Issues

Common issues include error codes, unresponsive displays, or temperature inaccuracies. Resetting the thermostat or checking wire connections often resolves these problems. Refer to the manual for specific solutions.

5.1 Common Error Codes and Solutions

The Honeywell RTH221B1021 thermostat may display error codes like E1, E2, or E3. E1 indicates a temperature range issue, while E2 signals a sensor problem. E3 suggests a power supply fault. To resolve these, ensure proper temperature settings for E1, check sensor connections for E2, and verify wiring for E3. If issues persist, reset the thermostat by removing batteries or checking the circuit breaker. Always refer to the manual for detailed troubleshooting steps.

5.2 Resetting the Thermostat

Resetting the Honeywell RTH221B1021 thermostat restores it to factory settings, erasing all programmed schedules and preferences. To reset, navigate to the menu, select the “Reset” option, and confirm. This process removes all custom settings, requiring you to re-program the thermostat afterward. Resetting is useful for resolving operational issues or preparing the device for a new installation. Ensure all settings are reconfigured to maintain optimal performance.

Maintenance and Upkeep

Regular cleaning ensures optimal performance. Use a soft cloth to wipe the display and exterior. Replace AA alkaline batteries every 12 months for smooth operation.

6.1 Cleaning the Thermostat

To maintain optimal performance, clean the Honeywell RTH221B1021 regularly. Turn off the power at the circuit breaker before cleaning. Gently wipe the thermostat’s display and surface with a soft, dry cloth. For tougher stains, slightly dampen the cloth with water, but avoid harsh chemicals or excessive moisture. Ensure the thermostat is dry before restoring power. Regular cleaning prevents dust buildup and ensures precise temperature control and smooth operation.

6.2 Replacing Batteries

Replace the batteries when the thermostat displays a low-battery warning. Turn off power to the system at the circuit breaker. Remove the old batteries from the compartment, typically located on the front or side. Insert new AAA alkaline batteries, ensuring correct polarity. Close the compartment and restore power. Check the LCD display to confirm operation. Properly dispose of used batteries, following local regulations for hazardous waste. Always use high-quality batteries for optimal performance.

Disposal Instructions

Ensure proper disposal of the Honeywell RTH221B1021 thermostat. If it contains mercury, follow local regulations for hazardous waste. Recycle responsibly and consult the manual for specific guidance.

7.1 Proper Disposal of Mercury Thermostats

For thermostats containing mercury, proper disposal is essential to prevent environmental harm. Check local regulations for hazardous waste disposal facilities. Carefully handle the mercury tube to avoid breakage. Wrap the thermostat securely in a sealed container to prevent leakage. Do not dispose of it in regular trash. Contact a certified hazardous waste collection center or refer to the owner’s manual for specific instructions. Visit Honeywell’s official website for detailed guidance on safe disposal practices.

User Reviews and Feedback

Users praise the Honeywell RTH221B1021 for its ease of use and energy efficiency, though some find it too basic or complex for advanced settings.

8.1 Customer Satisfaction Ratings

The Honeywell RTH221B1021 thermostat has received positive feedback, with an average customer satisfaction rating of 4.5 out of 5 stars. Users praise its ease of use, reliability, and energy-saving features. Many appreciate the intuitive LCD display and straightforward programming. Some customers highlight its durability and compatibility with various HVAC systems, making it a popular choice for home and office use.

8.2 Pros and Cons

The Honeywell RTH221B1021 thermostat is highly rated for its ease of use and energy efficiency. Users praise its clear LCD display, intuitive controls, and programmable scheduling. It is cost-effective and ideal for basic temperature control needs. However, some users find the design outdated and note the lack of smart home integration. Limited customization options are also a minor drawback for advanced users seeking more tailored settings.

The Honeywell RTH221B1021 thermostat is a reliable, efficient, and user-friendly solution for precise temperature control, offering simplicity and effectiveness for home and office environments.

9.1 Final Thoughts on the Honeywell RTH221B1021

The Honeywell RTH221B1021 is a practical and efficient programmable thermostat designed for simplicity and energy savings. With its LCD display and intuitive controls, it offers easy temperature management, making it ideal for homeowners seeking a straightforward solution. While it may lack advanced smart features, its reliability and ease of use make it a solid choice for those prioritizing basic functionality and energy efficiency.

Golf is a sport for life, offering a unique blend of challenge and enjoyment. A comprehensive PDF guide provides newcomers with essential rules, equipment setup, and techniques to start their journey. It simplifies the game, focusing on grip, stance, and basic swings, ensuring a solid foundation. Perfect for beginners, this resource helps players understand the fundamentals and enjoy the game while building skills and sportsmanship.

What is Golf and Why Play It?

Golf is a precision club and ball sport where players aim to hit balls into a series of holes using the fewest strokes possible. Unlike many sports, golf relies on individual integrity, as it is largely self-governed without referees. This makes it a game of honesty and sportsmanship. Golf is appealing for its unique blend of mental and physical challenge, offering a chance to connect with nature and build lasting friendships. It’s a sport for all ages and skill levels, teaching patience, focus, and perseverance. Playing golf provides a lifelong journey of improvement and enjoyment, making it a rewarding hobby for many.

The Benefits of Learning Golf

Golf offers numerous benefits, including improved physical health through regular exercise and fresh air. It enhances mental focus and patience, as players must concentrate on precise swings and strategies. The sport also fosters social connections, providing opportunities to meet new people and build relationships. Learning golf teaches discipline and integrity, as players are expected to follow rules and show respect for others. Additionally, golf can reduce stress and boost confidence, making it a rewarding activity for personal growth and enjoyment. These benefits make golf a valuable lifelong skill for players of all ages and backgrounds.

Golf Equipment Essentials

Golf requires specific gear, including clubs, balls, tees, and a bag. Proper attire like golf shoes and comfortable clothing enhances play. A well-prepared set ensures readiness for the course.

Golf Clubs: What You Need to Know

Golf clubs are a crucial part of the game, with a maximum of 14 allowed in a player’s bag. Beginners often start with a set including irons, woods, and a putter. Irons (3, 5, 7, 9, and sand) are used for approach shots, while woods (3 wood) are for long-distance tee shots. Hybrids and fairway woods can also be included for versatility. The putter is essential for rolling the ball on the green. Proper club selection and setup are vital for improving accuracy and consistency. Consulting a professional fitter ensures clubs are tailored to your swing and preferences, enhancing performance.

Golf Balls and Accessories

Golf balls are essential, with different types suited for various swing speeds and preferences. Beginners often opt for 2-piece balls for distance and forgiveness. Accessories like tees, ball markers, and gloves enhance play. A golf bag is necessary for carrying clubs, while divot tools and towels help maintain the course. Proper attire, including golf shoes, ensures stability and comfort. Accessories also include rangefinders and GPS devices for accurate yardage. These tools collectively improve performance and make the game more enjoyable, helping beginners adapt to the demands of golf with confidence and preparedness.

Dressing Appropriately for the Course

Dressing appropriately for the golf course is essential for both comfort and adherence to traditional etiquette. Beginners should opt for breathable, moisture-wicking clothing that allows freedom of movement. Collared shirts for men and modest tops for women are standard. Golf-specific pants, shorts, or skirts are recommended, avoiding jeans or overly casual attire; Proper golf shoes with soft spikes are crucial for stability and traction. Socks should be moisture-wicking to keep feet dry. A hat or visor can protect from the sun, while a lightweight rain jacket is a practical addition for unpredictable weather. Dressing appropriately ensures a respectful and enjoyable experience on the course.

Basic Rules and Etiquette

Golf relies on player integrity and respect for others. Key rules include counting all strokes, maintaining pace of play, and repairing ball marks. Etiquette emphasizes safety, fairness, and tradition.

Understanding the Fundamental Rules

Golf relies on player integrity, as there are no referees to enforce rules. Key principles include counting all strokes, playing in order, and maintaining the course. Players must repair ball marks on greens and bunker damage. The USGA and R&A provide official rules, but beginners can focus on a simplified version. Local rules may apply, such as preferred lies or out-of-bounds areas. Knowing these basics ensures fair play and respect for the game. Understanding rules is essential for maintaining pace of play and enjoying the game responsibly. Proper adherence fosters a positive experience for all players.

Etiquette on the Golf Course

Etiquette is essential for a positive golf experience. Players should dress appropriately, following course dress codes. Repair divots and rake bunkers to maintain the course. Always let faster groups play through to keep the pace of play. Avoid loud noises and keep phones on silent. Stand still and avoid casting shadows during others’ shots. Show respect for fellow players and the course environment. Proper etiquette ensures everyone enjoys the game and maintains the integrity of the sport. These practices foster a welcoming and courteous atmosphere for all golfers.

The Golf Swing Fundamentals

The golf swing relies on proper grip, stance, posture, alignment, and aim. These basics ensure consistency and effectiveness, forming the foundation for a successful and enjoyable game.

Grip, Stance, and Posture

A proper grip is essential, with hands positioned neutral or slightly left to promote consistent ball-striking. Stance involves feet shoulder-width apart, knees slightly bent for balance. Posture requires a slight spine angle, weight evenly distributed. These fundamentals ensure control and power, allowing for a smooth swing. Proper alignment and aim follow naturally, setting up for accurate shots. Mastering these basics is crucial for improving technique and minimizing errors. Regular practice and adjustments refine these elements, enhancing overall performance on the course. They form the cornerstone of a reliable and effective golf swing.

Alignment and Aim

Proper alignment and aim are critical for accurate shots. Stand with feet, knees, and shoulders parallel to the target line. Align the clubface squarely with the ball, ensuring the logo points toward the target. Consistent pre-shot routines help maintain focus and accuracy. Avoid common mistakes like aiming errors, which can lead to wayward shots. Practice checking alignment regularly to build muscle memory. Proper alignment enhances precision, reducing slices and hooks. It is the foundation for consistent play, helping beginners build confidence and improve overall performance on the course. Mastering this skill leads to better scoring and a more enjoyable game.

The Short Game

The short game focuses on shots near the green, involving chipping, pitching, and putting. Mastering these skills is essential for scoring and confidence. Proper techniques and practice build proficiency, helping beginners improve their overall performance and enjoyment of the game.

Chipping and Pitching Basics

Chipping and pitching are fundamental skills in the short game, essential for shots near the green. Chipping involves low, rolling shots, while pitching requires higher, softer landings. Proper stance, grip, and club selection are crucial. Beginners should practice these techniques to develop control and consistency. A PDF guide provides detailed instructions and drills to master these basics, helping improve scoring and overall performance on the course. Regular practice and patience are key to building confidence and skill in these areas of the game.

Mastering the Putt

Mastering the putt is crucial for improving your golf game, as it directly impacts scoring. A consistent pre-shot routine helps align your body and eyes with the target. Grip and stance should remain steady, with the clubface square to the hole. Practice controlled tempo and ball position to ensure a smooth stroke. Training aids like alignment tools can enhance accuracy. Focus on reading greens to judge speed and break. Mental patience and confidence are key. Regular practice on the putting green builds skill and consistency, helping you sink more putts and lower your score. It’s the final step to a great round.

Scoring and Par

Par is the predetermined number of strokes for a hole, serving as a benchmark to measure skill. Lower scores indicate better performance, making par a key goal.

How Scoring Works in Golf

Golf scoring is based on the number of strokes taken to complete each hole, with the goal of achieving the lowest total score. A scorecard records strokes per hole, and penalties for lost balls or hazards. The player with the fewest strokes at the end wins. Key terms include par (the standard strokes per hole), bogey (one stroke over par), and birdie (one under); Understanding scoring helps track progress and enjoy the game, making it essential for beginners to grasp these basics for accurate and fair play.

Understanding Par and Its Importance

Par is the predetermined number of strokes a skilled golfer should take to complete a hole or a round. It serves as a benchmark for measuring performance. Each hole has a specific par, determined by its length and obstacles. Understanding par is crucial as it helps track progress and set realistic goals. Beginners can aim to meet or beat par to gauge improvement. Par also fosters fair play, allowing players of all skill levels to compete by comparing scores relative to par. Grasping par is essential for enjoying the game and setting achievable targets for skill development and enjoyment.

Safety and Precautions

Always call “fore” to alert others nearby when a ball is heading off-target. Be watchful of surroundings to avoid accidents. Proper warm-ups prevent injuries, and handling equipment safely is essential to ensure a secure playing environment for everyone.

Safe Practices on the Course

Safety is paramount in golf. Always shout “fore” if a ball is heading toward someone. Be mindful of your surroundings to avoid accidents. Properly warm up to prevent injuries. Handle clubs and balls with care to ensure a secure playing environment. Avoid distractions while swinging and never hit a ball when others are nearby. Wear appropriate attire, including golf shoes with soft spikes, to maintain stability. Stay hydrated and prepared for changing weather conditions. Respecting these practices ensures a safe and enjoyable experience for all players on the course.

Learning Resources

Comprehensive PDF guides and e-books provide essential knowledge for beginners. These resources cover equipment setup, basic techniques, and rules. They help build a strong foundation for new players.

Recommended PDF Guides for Beginners

Beginners can benefit from comprehensive PDF guides that simplify golf basics. These resources cover essential rules, equipment setup, and techniques. They include chapters on grip, stance, and swings, making learning easier. Many guides focus on breaking down complex concepts into simple steps. Some even offer tips for teaching children, ensuring a family-friendly approach. These guides are designed to help newcomers build a strong foundation. They also cover scoring systems and etiquette. Downloadable and easy to access, these resources are perfect for self-paced learning. They provide a clear path to understanding the game and improving skills over time.

Practice Tips and Lessons

Consistent practice is key to improving your golf game. Start with short sessions focusing on grip, stance, and posture. Break your swing into parts, practicing each segment slowly. Begin with chipping and putting before moving to full swings. Consider lessons with PGA coaches for personalized feedback. Join group classes to learn alongside fellow beginners. Be patient and celebrate small progress. Regular practice helps build muscle memory and confidence. Dedication will lead to steady improvement, making the game more enjoyable. Remember, golf is a journey, and every practice session brings you closer to mastering the basics.

Hanuman Chalisa‚ a revered devotional hymn composed by Goswami Tulsidas‚ is a poetic ode to Lord Hanuman‚ embodying devotion‚ strength‚ and loyalty. Its verses‚ written in Hindi‚ resonate deeply with millions‚ offering spiritual solace and inspiration. The PDF format of Hanuman Chalisa in Hindi has become a popular choice for devotees‚ ensuring easy access and digital sharing of this sacred text.

1.1 What is Hanuman Chalisa?

Hanuman Chalisa is a sacred Hindu devotional hymn composed by Goswami Tulsidas in Awadhi‚ a dialect of Hindi. Consisting of 40 verses‚ it praises Lord Hanuman‚ extolling his virtues like courage‚ loyalty‚ and devotion. Widely recited in temples and homes‚ it is a powerful prayer that seeks blessings and strength. Its popularity endures‚ with millions finding solace and inspiration in its verses. Available in PDF format‚ it remains easily accessible for devotees worldwide.

1.2 Origin and Significance

Hanuman Chalisa‚ composed by Goswami Tulsidas in the 16th century‚ holds immense religious and cultural significance. Written in Awadhi‚ a Hindi dialect‚ it consists of 40 verses praising Lord Hanuman’s devotion‚ strength‚ and loyalty. Its recitation is believed to bring divine blessings‚ courage‚ and peace‚ making it a cherished prayer in Hindu tradition‚ now widely accessible in PDF format for devotees globally.

1.3 Why is it Important for Devotees?

Hanuman Chalisa holds profound significance for devotees‚ offering spiritual strength‚ courage‚ and mental peace. Its recitation is believed to ward off troubles and attract divine blessings. The PDF format in Hindi ensures easy accessibility‚ allowing devotees to carry and recite the hymn anytime‚ making it an integral part of daily worship and a source of inspiration for millions worldwide.

Structure of Hanuman Chalisa

Hanuman Chalisa is a 40-verse prayer in Hindi‚ featuring rhythmic couplets. Its poetic structure makes it melodious and easy to recite. The PDF format preserves this traditional structure‚ allowing convenient digital access for devotees worldwide.

2.1 Number of Verses

Hanuman Chalisa consists of 40 verses‚ skillfully composed by Goswami Tulsidas in the Awadhi language. It includes a Doha at the beginning and a final verse seeking refuge in Lord Hanuman. This structured format‚ preserved in the PDF version‚ enhances its recitation and spiritual impact for devotees.

2.2 Language and Rhythm

The Hanuman Chalisa is composed in the Awadhi dialect of Hindi‚ known for its rhythmic and melodious verses. The rhythmic pattern enhances the recitation experience‚ making it easier for devotees to follow and remember. The PDF format in Hindi maintains the authentic pronunciation and cultural essence‚ ensuring a meaningful spiritual connection. Devotees often recite these verses in unison during prayers‚ fostering unity and collective devotion.

2.3 Key Themes and Messages

The Hanuman Chalisa emphasizes devotion‚ courage‚ and loyalty through its verses. It highlights Lord Hanuman’s unwavering dedication to Lord Rama and his divine grace. The hymn also conveys the power of faith and the triumph of good over evil. Its messages inspire devotees to cultivate resilience and trust in the divine‚ fostering a deeper spiritual connection and emotional solace.

Benefits of Reading Hanuman Chalisa

Reading Hanuman Chalisa fosters spiritual growth‚ mental peace‚ and emotional strength. It helps devotees connect with divine grace‚ offering solace and inspiration in daily life.

3.1 Spiritual Benefits

Reciting Hanuman Chalisa in Hindi PDF fosters deep spiritual connection‚ enhancing devotion and faith. It is believed to ward off negativity‚ grant divine blessings‚ and bring inner peace‚ helping seekers attain spiritual enlightenment and strength through Lord Hanuman’s divine grace‚ as highlighted in its verses.

3.2 Emotional and Mental Peace

Reciting Hanuman Chalisa in Hindi PDF brings emotional solace and mental tranquility. Its verses alleviate stress‚ offering comfort and inner harmony. The rhythmic chanting helps devotees connect deeply‚ fostering a sense of calm and emotional balance‚ making it a powerful tool for mental well-being and spiritual upliftment in today’s fast-paced world.

3.4 How it Inspires Devotion

Hanuman Chalisa in Hindi PDF ignites deep devotion by glorifying Lord Hanuman’s unwavering loyalty and strength. Its verses‚ composed by Tulsidas‚ evoke a profound connection to the divine. The hymn’s rhythmic and poetic structure makes it easy to chant‚ fostering a sense of reverence and spiritual dedication. Regular recitation strengthens faith and inspires devotees to embody Hanuman’s virtues in daily life.

How to Download Hanuman Chalisa PDF in Hindi

Visit trusted websites like spiritual portals or religious platforms. Search for “Hanuman Chalisa PDF in Hindi” and download from verified sources to ensure authenticity and accessibility.

4.1 Reliable Sources for Download

Trustworthy platforms include official religious websites‚ e-book platforms‚ and spiritual apps. Look for sources with verified credentials and positive reviews. Ensure authenticity by checking for proper formatting and the presence of the author’s name‚ Goswami Tulsidas. Avoid unverified links to maintain quality and safety during the download process.

4.2 Step-by-Step Download Guide

Visit a trusted website‚ such as official religious portals or e-book platforms. Search for “Hanuman Chalisa PDF in Hindi.” Select the desired version from the search results. Locate the download button‚ often found on the left side. Click to initiate the download‚ choose a save location‚ and wait for completion. Ensure the file is verified for authenticity before opening.

4.3 Ensuring Authenticity

Verify the credibility of the source by choosing trusted websites or religious platforms. Look for official seals or certifications. Compare the content with known authentic versions of Hanuman Chalisa. Ensure the PDF is free from unauthorized alterations or malware by scanning it with antivirus software before opening. This ensures a genuine and safe download experience for devotees seeking the sacred text.

Popular Platforms for Hanuman Chalisa PDF

Trusted religious websites‚ apps‚ and platforms offer free Hanuman Chalisa PDF downloads in Hindi. These sources ensure easy access and authenticity‚ catering to devotees worldwide seamlessly.

5.1 Websites Offering Free Downloads

Several websites provide free Hanuman Chalisa PDF downloads in Hindi. Platforms like HolyBooks.com and DharmaKshetra.com are reliable sources. These sites offer easy navigation‚ ensuring quick access to the text. Many include features like downloadable buttons and compatibility with mobile devices. Some also offer translations or interpretations for deeper understanding‚ making them popular among devotees seeking both convenience and authenticity.

5.2 Apps Providing Digital Access

Apps like Hanuman Chalisa Audio and Hindu Devotional Apps offer digital access to Hanuman Chalisa in Hindi. These apps provide PDF versions‚ often accompanied by audio recitations. Users can download or stream the content‚ ensuring accessibility anywhere. Many apps also feature offline access‚ making them convenient for devotees seeking spiritual connection on the go. Their user-friendly interfaces enhance the overall experience.

5.3 Trusted Religious Portals

Trusted religious portals like Shri Saibaba Sansthan Trust and Kumbh Mela Official offer authentic downloads of Hanuman Chalisa in Hindi PDF. These platforms are renowned for their credibility and spiritual focus‚ ensuring devotees access genuine content. They often provide free downloads‚ making it easy for millions to connect with this sacred hymn. Their user-friendly interfaces and reliable sources make them a preferred choice for seekers of divine texts.

Understanding the Language of Hanuman Chalisa

Hanuman Chalisa‚ originally written in Awadhi‚ is widely available in Hindi‚ making it accessible to millions. Its poetic style and devotional tone resonate deeply‚ connecting devotees to Lord Hanuman.

6.1 Importance of Hindi in the Text

Hindi‚ as the primary language of Hanuman Chalisa‚ ensures its accessibility to a vast audience in India and beyond. Its simplicity and cultural significance make the hymn resonate deeply‚ fostering a spiritual connection among devotees. The use of Hindi in the PDF format preserves its traditional essence‚ allowing millions to recite and connect with Lord Hanuman’s divine qualities effectively.

6.2 Transliterations for Non-Hindi Speakers

Transliterations of Hanuman Chalisa in Hindi provide a bridge for non-Hindi speakers‚ enabling them to recite the hymn accurately. Tools like Notta offer transliterations in over 104 languages‚ making the text accessible globally. This feature ensures that devotees worldwide can pronounce and understand the verses‚ fostering a deeper spiritual connection to Lord Hanuman‚ regardless of their linguistic background.

6.3 Cultural Relevance of the Language

The use of Hindi in Hanuman Chalisa holds profound cultural significance‚ as it connects devotees to India’s rich spiritual heritage. Composed in Awadhi‚ a dialect close to Hindi‚ the text embodies traditional devotional poetry. Its language resonates emotionally with millions‚ making it accessible and relatable. This linguistic roots ensure the hymn remains a vital part of India’s cultural and religious identity‚ transcending generations.

Hanuman Chalisa in Digital Format

The digital format of Hanuman Chalisa in Hindi enhances accessibility‚ enabling devotees to easily share and read the text on various devices‚ fostering modern worship practices.

7.1 Advantages of PDF Format

The PDF format of Hanuman Chalisa in Hindi offers clarity in text and layout‚ ensuring the sacred verses are easily readable. It is portable‚ allowing devotees to carry the text on devices like smartphones and tablets. The format also enables seamless sharing via email or messaging apps‚ making it accessible to a broader audience. Additionally‚ PDFs maintain the original structure and integrity of the hymn‚ preserving its spiritual significance for digital generations.

7.2 Customization Options

The Hanuman Chalisa PDF in Hindi allows users to customize their experience by adjusting font sizes for readability. Devotees can highlight verses‚ add bookmarks‚ and even annotate sacred lines for personal reflection. Some PDFs also support night mode‚ reducing eye strain during late-night recitals. These features enhance accessibility and make the text adaptable to individual preferences‚ ensuring a deeper connection with the divine hymn.

7.3 Sharing and Accessibility

The Hanuman Chalisa PDF in Hindi can be easily shared via email‚ messaging apps‚ or social media‚ ensuring widespread accessibility. Its digital format allows devotees to access it on smartphones‚ tablets‚ or computers‚ making it convenient for daily recitation. Additionally‚ the PDF’s lightweight size ensures quick downloads‚ even in areas with limited internet connectivity‚ fostering spiritual connection for all.

The Role of Hanuman Chalisa in Daily Worship

Hanuman Chalisa is integral to daily worship‚ recited during morning and evening rituals to invoke divine blessings. Its verses bring spiritual strength and focus‚ enriching devotional practices.

8.1 Morning and Evening Recitation

Morning and evening recitation of Hanuman Chalisa is an integral part of daily worship for many devotees. It is believed to bring spiritual strength‚ mental peace‚ and divine blessings. The PDF version of Hanuman Chalisa in Hindi makes it convenient for devotees to recite the hymn at any time‚ ensuring consistency in their daily worship routine and fostering a deeper connection with Lord Hanuman.

8.2 Rituals and Practices

Devotees often perform specific rituals while reciting Hanuman Chalisa‚ such as offering flowers‚ lighting diyas‚ and chanting before an idol of Lord Hanuman. The PDF version in Hindi facilitates these practices by providing clear‚ accessible text for recitation. Many believe that consistent chanting‚ especially during rituals‚ strengthens faith and invokes divine blessings‚ enhancing the spiritual experience of worship and devotion.

8.3 Incorporating it into Puja

The Hanuman Chalisa PDF in Hindi is often integrated into daily and special Puja rituals‚ offering devotees a convenient format for recitation. Its digital accessibility ensures uninterrupted worship‚ allowing easy sharing among participants. This format maintains the sanctity of traditional practices while embracing modern convenience‚ making it a seamless addition to both home and temple Pooja ceremonies.

Cultural and Religious Impact

The Hanuman Chalisa PDF in Hindi has profoundly impacted cultural and religious practices‚ making the sacred text accessible to a broader audience‚ bridging tradition with modern convenience‚ and strengthening devotion globally.

9.1 How it Unites Devotees

The Hanuman Chalisa PDF in Hindi fosters a sense of unity among devotees worldwide‚ enabling collective recitation and shared spiritual experiences. Its digital accessibility transcends geographical boundaries‚ connecting millions through a common faith and devotion to Lord Hanuman‚ strengthening bonds within the global Hindu community and inspiring collective worship and reflection.

9.2 Its Role in Festivals and Celebrations

The Hanuman Chalisa PDF in Hindi plays a pivotal role in Hindu festivals‚ particularly during Hanuman Jayanti‚ enhancing devotional practices. Its digital format ensures widespread accessibility‚ allowing devotees to recite it during pujas and processions. This shared recitation strengthens community bonds and fosters spiritual unity‚ making it an integral part of festive celebrations and cultural traditions.

9.3 Influence on Art and Music

The Hanuman Chalisa PDF in Hindi has profoundly influenced art and music‚ inspiring numerous devotional compositions and visual interpretations; Its verses have been set to melodious tunes‚ creating popular bhajans and kirtans. Digital access to the PDF has facilitated the creation of multimedia art‚ combining text with visuals and audio‚ thus enriching the cultural and spiritual experience of devotees globally.

The Hanuman Chalisa PDF in Hindi is a timeless spiritual treasure‚ offering devotion‚ strength‚ and peace. Its digital format enhances accessibility‚ preserving its essence for modern devotees worldwide.

10.1 Final Thoughts on Hanuman Chalisa PDF

The Hanuman Chalisa PDF in Hindi serves as a convenient and accessible spiritual resource‚ allowing devotees to carry the sacred hymn wherever they go. Its digital format ensures that the timeless teachings of Lord Hanuman remain easily accessible‚ catering to both traditional and modern preferences. This PDF is a valuable tool for daily worship and reflection‚ preserving the essence of devotion in a contemporary world.

10.2 Encouragement to Explore Further

Exploring the Hanuman Chalisa PDF in Hindi invites deeper spiritual connection and understanding. Delve into its verses‚ reflect on their meanings‚ and incorporate its teachings into daily life. Engage with communities‚ attend recitals‚ and share its wisdom with others. Let this sacred text inspire personal growth and devotion‚ serving as a timeless guide for spiritual enrichment and emotional harmony.

The Norton Anthology of African American Literature provides a comprehensive collection of works, spanning six historical periods, with contributions from 120 writers, now available in PDF format.

1.1 Overview of the Anthology

The Norton Anthology of African American Literature is a comprehensive collection of works spanning six historical periods, from slavery to modernism. It includes poetry, prose, drama, and fiction by 120 writers, with notable contributions from figures like Phillis Wheatley and Langston Hughes. Available in PDF format, it offers a detailed exploration of African American literary history, with bibliographical references and an index for easy navigation.

1.2 Significance of the Anthology in African American Literary Studies

The Norton Anthology of African American Literature is a cornerstone in the field, preserving voices from slavery to modernism. It offers a comprehensive exploration of identity, race, and freedom, showcasing works by 120 writers. Available in PDF, it serves as an essential resource for scholars and students, highlighting the evolution of African American literature and its cultural significance.

1.3 Purpose and Scope of the Anthology

The anthology aims to provide a diverse and comprehensive collection of African American literary works, spanning six historical periods. It includes poetry, prose, drama, and fiction, offering insights into themes like identity and freedom. Available in PDF and multiple editions, it covers works from iconic figures like Langston Hughes to lesser-known writers, ensuring a broad representation of voices and literary traditions.

Historical Context of the Anthology

The anthology spans six historical periods, from slavery to Modernism, capturing the evolution of African American literature and its cultural significance over time.

2.1 Key Periods Covered: Slavery and Freedom, Reconstruction, Harlem Renaissance

The anthology spans three pivotal eras: Slavery and Freedom, marked by early narratives like Phillis Wheatley and Frederick Douglass; Reconstruction, exploring themes of identity and liberation; and the Harlem Renaissance, showcasing Langston Hughes and Zora Neale Hurston amidst a cultural explosion. These periods highlight the evolution of African American voices, from resilience under oppression to artistic flourishing.

2.2 The Evolution of African American Literature Through Different Eras

African American literature evolves from early narratives of slavery and freedom to the vibrant creativity of the Harlem Renaissance. The anthology traces this journey, showcasing the shift from testimonial accounts to poetic expressions of identity, race, and freedom. Realism and Naturalism emerge, reflecting societal challenges, while modernist influences expand the scope, capturing the diverse voices and experiences of Black America across centuries.

2.3 The Role of the Anthology in Preserving Historical Voices

The anthology serves as a vital archive, preserving works from pivotal African American writers like Phillis Wheatley and Frederick Douglass. By compiling these voices, it ensures their legacy endures, offering insights into the struggles and triumphs of Black history. This collection not only educates but also honors the literary and cultural heritage, making it an essential resource for understanding the African American experience.

Editors and Contributors

Edited by Henry Louis Gates Jr. and Valerie A. Smith, the anthology features works from notable contributors like W.E.B. Du Bois and Langston Hughes, ensuring diverse perspectives.

3.1 Henry Louis Gates Jr. and Valerie A. Smith: Their Contributions as Editors

Henry Louis Gates Jr. and Valerie A. Smith are renowned scholars who meticulously curated the anthology, ensuring a diverse representation of African American voices. Their expertise in literary history and critical analysis has been instrumental in shaping the anthology’s structure and content, offering readers a profound understanding of the cultural and historical significance of the works included.

3.2 Notable Contributors and Their Works

The anthology features works by iconic figures such as W.E.B. Du Bois, Zora Neale Hurston, Langston Hughes, and Toni Morrison. Their contributions include seminal texts like The Souls of Black Folk, Their Eyes Were Watching God, and Beloved. These works encapsulate the richness and diversity of African American literary expression, offering profound insights into themes of identity, race, and cultural resilience across generations.

3.3 The Collaborative Effort Behind the Anthology

The anthology is a result of a collaborative effort by renowned editors Henry Louis Gates Jr. and Valerie A. Smith, alongside scholars William L. Andrews, Kimberly Benston, and Brent Hayes Edwards. Their collective expertise ensured a diverse and representative selection of texts, reflecting the breadth of African American literary history and cultural heritage in a cohesive and accessible format.

Structure and Organization of the Anthology

The anthology is divided into two volumes, covering six historical periods, from slavery to modernism, with detailed bibliographical references and a comprehensive index for ease of navigation.

4.1 Division into Volumes and Sections

The anthology is divided into two volumes, each organized chronologically, covering six historical periods: Slavery and Freedom, Reconstruction, Harlem Renaissance, Realism, Naturalism, and Modernism. Volume 1 spans from early writers like Phillis Wheatley to the Harlem Renaissance, while Volume 2 covers the 20th century to contemporary works. Each section includes introductions and headnotes, providing historical and literary context, with works by over 120 contributors.

4.2 Notable Works and Authors Featured

The anthology showcases works by influential figures like Phillis Wheatley, Frederick Douglass, Langston Hughes, Zora Neale Hurston, and Toni Morrison. Notable works include Hughes’s poetry, Hurston’s Their Eyes Were Watching God, and Morrison’s Beloved. These selections highlight the diversity of African American literary expression, spanning poetry, prose, and drama, and reflecting the richness of the tradition from early voices to contemporary masters.

4.3 Bibliographical References and Index

The anthology includes extensive bibliographical references, providing scholars with sources for further exploration. A detailed index ensures easy navigation through the vast collection of works and authors. These features enhance its utility as both a teaching tool and a resource for academic research, making it an indispensable reference for studying African American literature in depth and context.

Key Themes and Genres

The anthology explores themes of identity, race, and freedom, showcasing poetry, prose, and drama. It reflects influences from Realism, Naturalism, and Modernism, enriching the literary landscape.

5.1 Exploration of Themes Such as Identity, Race, and Freedom

The anthology delves into profound themes of identity, race, and freedom, offering insights into the African American experience. Through diverse voices, it traces the journey from oppression to liberation, highlighting resilience and cultural richness. These themes are central to understanding the historical and social contexts that shaped African American literature, making the anthology a vital resource for scholars and readers alike.

5.2 Representation of Different Literary Genres: Poetry, Prose, Drama

The anthology showcases a diverse range of genres, including poetry, prose, and drama, spanning from the 16th century to the 20th century. It features works by iconic figures such as Phillis Wheatley, Frederick Douglass, Langston Hughes, Zora Neale Hurston, and Lorraine Hansberry. These contributions highlight the evolution of African American literary expression, enriching the anthology’s historical and cultural depth.

5.3 The Influence of Realism, Naturalism, and Modernism

The anthology highlights the impact of Realism, Naturalism, and Modernism on African American literature, showcasing works that reflect these movements. Realism captures everyday life, while Naturalism explores social challenges. Modernism introduces experimental styles, seen in works by Langston Hughes and Zora Neale Hurston. These genres enrich the anthology, offering diverse perspectives on race, identity, and cultural transformation across different eras.

Impact and Reception

The Norton Anthology of African American Literature is a foundational text, shaping academic and cultural understanding of Black experiences. Its educational influence is profound, with widespread adoption in curricula and positive scholarly reviews, making it accessible in PDF and other formats for global engagement.

6.1 Academic and Cultural Significance of the Anthology

The Norton Anthology of African American Literature is a cornerstone of academic and cultural discourse, offering a definitive collection of works spanning from slavery to modernism. Its comprehensive coverage of key historical periods, such as the Harlem Renaissance, has made it indispensable in curriculum development. Available in PDF, it fosters global accessibility, enabling scholars and readers to engage with foundational texts that explore Black identity, resilience, and cultural heritage, bridging past and present.

6.2 Reviews and Feedback from Scholars and Readers

Scholars and readers have praised the anthology for its comprehensive coverage of African American literary history, spanning six key periods. Reviewers highlight its inclusion of seminal works by figures like Phillis Wheatley, Frederick Douglass, and Langston Hughes. The PDF format has enhanced accessibility, making it a vital resource for both academic and personal exploration. Feedback underscores its enduring relevance and educational impact.

The Norton Anthology of African American Literature is a foundational text in many educational institutions, shaping syllabi for courses on African American studies and literature. Its comprehensive coverage of six key historical periods makes it an essential resource for curriculum development. The anthology’s availability in PDF format has further enhanced its accessibility, enabling educators and students to integrate its wealth of materials seamlessly into academic programs.

Availability and Editions

6.3 The Anthology’s Role in Education and Curriculum Development

The Norton Anthology of African American Literature is a cornerstone in educational curricula, offering a diverse range of texts that enhance teaching and learning. Its availability in PDF format has made it easily accessible for students and educators, facilitating its integration into academic programs and fostering deeper engagement with African American literary traditions across various educational institutions.

7.1 Different Editions: First, Second, and Third

The Norton Anthology of African American Literature is available in three editions, with the first published in 1996, the second in 2004, and the third in 2014. Each edition expands the scope, incorporating more voices and contemporary works. The third edition, edited by Henry Louis Gates Jr. and Valerie A. Smith, is divided into two volumes, offering a comprehensive collection of texts and updated scholarship. The PDF version of the third edition is widely accessible online.

7.2 Formats: Hardcover, Paperback, and Digital (PDF)

The Norton Anthology of African American Literature is available in hardcover, paperback, and digital PDF formats. Hardcover and paperback editions offer tactile reading experiences, while the PDF version provides digital convenience. The PDF format is particularly popular for its accessibility on multiple devices, enabling easy reference and study. All formats include the same comprehensive content, ensuring readers can engage with the anthology in their preferred medium.

7.3 Where to Access the Anthology: Libraries, Bookstores, and Online Platforms

The Norton Anthology of African American Literature is widely available in libraries, bookstores, and online platforms. Libraries often carry physical copies, while bookstores offer both hardcover and paperback editions. Online platforms like Amazon, Google Books, and JSTOR provide digital access, including the PDF version. This accessibility ensures readers can easily obtain the anthology in their preferred format.

Calculus 3 problems and solutions are essential for mastering advanced mathematical concepts․ LitRes offers PDF resources like Problems and Solutions in Mathematical Finance and Stochastic Calculus․ Paults Notes provide detailed solutions to multivariable calculus and differential equations․ These materials cover vector operations, partial derivatives, and multiple integrals, aiding in exam preparation and deep understanding of complex topics․

1․1 Overview of Calculus 3 Topics

Calculus 3 explores advanced mathematical concepts, including vector operations, partial derivatives, and multiple integrals․ It delves into vector calculus, differential equations, and series, providing tools for solving complex problems․ Topics like dot and cross products, geometric interpretations, and optimization using partial derivatives are central․ Multiple integrals, including double and triple integrals, are covered, along with transformations․ The subject also introduces line integrals, Green’s Theorem, and boundary value problems․ These topics are essential for fields like physics, engineering, and advanced mathematics, requiring a strong foundation in earlier calculus concepts․

1․2 Importance of Practice Problems in Learning Calculus 3

Practice problems are vital for mastering Calculus 3, as they reinforce understanding of complex concepts like vector operations and partial derivatives․ Solving problems helps apply theoretical knowledge to real-world scenarios, enhancing problem-solving skills․ Regular practice builds confidence and familiarity with various problem types, preparing students for exams and advanced studies; Resources such as Problems and Solutions in Mathematical Finance and Stochastic Calculus provide comprehensive exercises․ Platforms like LitRes and Paul’s Notes offer detailed solutions, aiding in self-study and deeper comprehension of challenging topics․

Vector Operations and Applications

Vector operations, including addition, dot, and cross products, are fundamental in Calculus 3․ Applications include solving systems of equations and optimization problems, with resources like LitRes and Paul’s Notes providing comprehensive practice materials․

2․1 Vector Addition, Dot Product, and Cross Product

Vector addition involves combining vectors component-wise, while the dot product measures the angle between two vectors․ The cross product yields a perpendicular vector․ Resources like LitRes and Paul’s Notes provide detailed solutions to problems involving these operations․ Geometric interpretations, such as projecting vectors or finding perpendicular vectors, are also covered․ These concepts are essential for solving systems of equations and optimization problems in physics and engineering․ Practice materials include exercises on vector calculus, ensuring a solid understanding of these fundamental operations․

2․2 Geometric Interpretations of Vector Operations

Geometric interpretations of vector operations provide visual insights into their applications․ The dot product reveals the projection of one vector onto another, while the cross product generates a perpendicular vector․ Resources like LitRes and Paul’s Notes offer problems and solutions that explore these geometric meanings․ For instance, calculating the area of a parallelogram using the cross product or understanding the angle between vectors using the dot product․ These interpretations are crucial in physics and engineering, enabling the solution of real-world problems involving forces, torques, and spatial orientations․ Practice materials ensure a deep understanding of these geometric applications․

Partial Derivatives and Their Applications

Partial derivatives measure the rate of change of a function with respect to one variable․ Resources like LitRes and Paul’s Notes provide problems and solutions covering their computation and applications in optimization, essential for mastering calculus concepts․

3․1 Computing Partial Derivatives

Computing partial derivatives involves measuring the rate of change of a multivariable function with respect to one variable․ Resources like LitRes and Paul’s Notes provide detailed solutions to problems involving partial derivatives․ These materials cover key concepts such as limit definitions, partial derivative rules, and applications in optimization․ For example, Problems and Solutions in Mathematical Finance offers insights into stochastic calculus, while Paul’s Notes includes step-by-step solutions for calculus III problems․ These resources help students master the computation of partial derivatives and their practical applications in fields like physics and engineering․

3․2 Optimization Problems Using Partial Derivatives

Partial derivatives are fundamental in solving optimization problems, where they help identify local maxima, minima, and saddle points․ Resources like Problems and Solutions in Mathematical Finance and Paul’s Notes offer detailed solutions to such problems․ These materials cover methods for finding critical points and applying second derivative tests․ For instance, LitRes provides examples of optimizing multivariable functions under constraints, while Paul’s Notes includes step-by-step solutions for real-world applications․ These tools are invaluable for students mastering optimization techniques in calculus and their practical uses in science and engineering․

Multiple Integrals in Calculus 3

Multiple integrals extend calculus to higher dimensions, enabling volume and surface integrations․ Resources like LitRes and Paul’s Notes offer problem sets and solutions for double and triple integrals․

4․1 Double and Triple Integrals

Double and triple integrals are fundamental in Calculus 3 for solving complex problems involving volume and surface integrations․ These integrals extend the concepts of single-variable calculus to multiple dimensions, enabling the calculation of volumes and integrals over curved surfaces․ Resources like LitRes and Paul’s Notes offer comprehensive PDF guides with detailed solutions to double and triple integral problems․ These materials cover a wide range of applications, from basic volume calculations to advanced surface integrations, providing students with essential tools to master these challenging topics effectively․

4․2 Changing Variables in Multiple Integrals

Changing variables in multiple integrals is a powerful technique to simplify complex integration problems․ It involves transforming coordinates, such as switching from Cartesian to polar or spherical systems, to make calculations more manageable․ Resources like LitRes and Paul’s Notes provide detailed solutions and examples of variable transformations, including Jacobian determinants and coordinate conversions․ These materials are invaluable for understanding how to apply these methods effectively in various mathematical and real-world applications, ensuring a deeper grasp of integral transformations and their practical uses․

Vector Calculus and Differential Equations

Vector calculus and differential equations are core topics, with resources like Paul’s Notes offering solutions to boundary value problems and line integrals using Green’s Theorem․

5․1 Line Integrals and Green’s Theorem

Line integrals and Green’s Theorem are fundamental in vector calculus, enabling the evaluation of vector fields along curves and converting them into double integrals․ Resources like LitRes and Paul’s Notes provide detailed solutions to problems involving line integrals, parametrization, and circulation․ Green’s Theorem simplifies flux and curvature calculations, with applications in physics and engineering․ Practice problems often involve computing work done by forces and verifying the theorem for various vector fields․ These materials offer step-by-step solutions, aiding students in mastering these concepts for exams and real-world applications․

5․2 Solutions to Boundary Value Problems

Solutions to boundary value problems involve determining functions that satisfy specific conditions at the boundaries of a domain․ Resources like LitRes and Paul’s Notes offer detailed solutions to ODE systems and nonlinear boundary value problems․ These materials cover reducing linear problems to Cauchy problems and addressing complex scenarios․ Practice problems often focus on verifying solutions and applying conditions․ The internet provides extensive study guides and formula sheets, aiding students in mastering these concepts for exams and advanced applications in physics and engineering․

Series and Sequences in Calculus 3

Series and sequences are fundamental in Calculus 3, involving convergence tests and power series․ Resources like LitRes and Paul’s Notes provide detailed solutions and study guides․

6․1 Convergence Tests for Series

Convergence tests for series are crucial in determining the behavior of infinite series․ The comparison test, ratio test, and root test are essential tools․ Resources like LitRes offer PDF guides with detailed solutions, while Paul’s Notes provide step-by-step explanations․ These materials cover tests for positive-term series, alternating series, and power series․ Practice problems and solutions help students master concepts like absolute convergence and conditional convergence․ Online platforms also offer free problem sets for self-study, ensuring comprehensive understanding of series convergence in Calculus 3․

6․2 Power Series and Their Applications

Power series are fundamental in representing functions and solving complex mathematical problems․ They are used to expand functions like exponential and trigonometric functions․ Resources like LitRes offer PDF guides with detailed solutions, while Paul’s Notes provide step-by-step explanations․ These materials cover applications in differential equations, physics, and engineering․ Practice problems and solutions help students master concepts like radius of convergence and Taylor series․ Online platforms also offer free problem sets for self-study, ensuring comprehensive understanding of power series in Calculus 3․

Calculus 3 Problems and Solutions PDF Resources

PDF resources like LitRes and Paul’s Notes offer comprehensive guides for Calculus 3, including detailed solutions․ These materials cover vector operations, partial derivatives, and multiple integrals, aiding in exam preparation and deep understanding of complex topics․

7․1 Recommended PDF Study Guides for Calculus 3

Several PDF study guides are highly recommended for Calculus 3․ LitRes offers Problems and Solutions in Mathematical Finance and Stochastic Calculus by Eric Chin, providing detailed solutions․ Additionally, a comprehensive formula sheet by MI Gomoyunov includes over 30 essential formulas for vector operations, partial derivatives, and multiple integrals․ Paul’s Notes also provides extensive solutions to multivariable calculus and differential equations problems․ These resources are invaluable for students seeking to enhance their understanding and prepare for exams effectively․

7․2 Online Platforms Offering Free Calculus 3 Problem Sets

Several online platforms provide free Calculus 3 problem sets․ Paul’s Notes offers detailed solutions to multivariable calculus and differential equations․ Additionally, practice problems and solutions are available on educational websites like Lamar University․ A formula sheet by MI Gomoyunov covers essential topics such as vector operations and partial derivatives․ These resources are freely accessible, making them ideal for students seeking to practice and deepen their understanding of Calculus 3 concepts without additional costs․

Overview of Conceptual Physics 13th Edition

Conceptual Physics, 13th Edition, by Paul G. Hewitt, is a renowned textbook that blends engaging visuals and updated content to make physics accessible and enjoyable for students.

1.1 Key Features of the 13th Edition

The 13th Edition of Conceptual Physics offers engaging visuals, updated content, and interactive learning tools. It includes Hewitt-Drew-It screencasts, which provide fun and informative explanations of complex concepts. The book focuses on practical applications, making physics relatable and accessible. With a robust structure, it covers essential topics in mechanics, thermodynamics, and modern physics. The edition also features bibliographical references and an index for easy navigation. These enhancements ensure a comprehensive and enjoyable learning experience for students.

1.2 Author and Publication Details

Conceptual Physics, 13th Edition, is authored by Paul G. Hewitt, a renowned educator known for making physics accessible. Published by Pearson, the Global Edition is tailored for an international audience. The book holds ISBN-10: 1292437332 and ISBN-13: 978-1292437330. First published in 2023, it remains a trusted resource for students and educators worldwide. Hewitt’s engaging approach and clear explanations have made this edition a popular choice for understanding fundamental physics concepts.

Where to Find the Conceptual Physics 13th Edition PDF

The PDF of Conceptual Physics, 13th Edition can be sourced from official publishers like Pearson or third-party platforms such as online libraries and educational forums.

2.1 Official Sources for Download

Official sources for downloading the PDF of Conceptual Physics, 13th Edition include the publisher’s website, Pearson, and authorized online bookstores like Amazon or Barnes & Noble. These platforms offer legal and secure access to the e-book, ensuring quality and authenticity. Additionally, Pearson provides an eText version through their official platform, allowing students to access the material digitally. Always verify the source’s legitimacy to avoid unauthorized downloads and respect copyright laws.

2.2 Third-Party Platforms and Availability

Third-party platforms like Google Books, Scribd, and Open Library offer access to Conceptual Physics, 13th Edition in PDF format. These platforms often provide free downloads, though availability may vary. Some sites require user registration or subscription for full access. Additionally, platforms like Internet Archive host PDF versions, including single-page processed JP2 ZIP and TORRENT options. While convenient, users must ensure downloads comply with copyright laws and respect intellectual property rights. Always verify the source’s legitimacy to avoid unauthorized content.

Content and Structure of the Book

Conceptual Physics, 13th Edition covers fundamental physics topics, including mechanics, Newton’s laws, and modern applications, with engaging visuals like Hewitt-Drew-It screencasts and bibliographical references.

3.1 Chapter Highlights and Topics Covered

Conceptual Physics, 13th Edition covers a wide range of topics, starting with an introduction to science and moving through mechanics, Newton’s laws, energy, and modern applications. The book is divided into clear sections, with chapters on motion, forces, and thermal physics, ensuring a logical progression of concepts. It also includes engaging visuals like Hewitt-Drew-It screencasts and practical examples to enhance understanding. Bibliographical references and an index are provided for further study, making it a comprehensive resource for students.

3.2 Unique Learning Resources Included

The 13th Edition includes Hewitt-Drew-It screencasts, which provide engaging visual explanations of complex physics concepts. Additionally, it offers interactive simulations and problem-solving tools to enhance student engagement. The book also features real-world applications, connecting theoretical knowledge to practical scenarios. These resources create a dynamic learning environment, making the material more accessible and enjoyable for students. The integration of multimedia elements ensures a well-rounded educational experience, catering to diverse learning styles and preferences.

Importance of Respecting Copyright Laws

Respecting copyright laws ensures legal compliance and supports authors. Downloading copyrighted materials like Conceptual Physics 13th Edition without authorization is illegal and undermines creator rights.

4.1 Legal Considerations for PDF Downloads

Downloading copyrighted materials like the Conceptual Physics 13th Edition PDF without authorization violates copyright laws, potentially leading to legal consequences. Publishers and authors rely on legitimate sales to sustain their work, and unauthorized distribution deprives them of rightful income.

Always purchase or access the eBook through official channels to ensure compliance with copyright regulations and support the creators. Illegal downloads not only risk legal penalties but also undermine the quality and availability of educational resources.

4.2 Ethical Practices for Educational Materials

Respecting copyright and ethical practices when accessing educational materials like the Conceptual Physics 13th Edition PDF is essential. Purchasing or accessing the book through official channels ensures you support the authors and publishers who invest in creating high-quality educational content.

Illegal downloads not only violate laws but also harm the education community by reducing incentives for publishers to produce affordable and accessible resources. Ethical access promotes fairness and sustains the development of valuable learning tools for future students.

Digital Accessibility and Formats

The 13th Edition is available in PDF (encrypted) and other digital formats, ensuring compatibility with e-readers and mobile devices while protecting copyright through DRM.

5.1 E-Book Formats and Compatibility

The 13th Edition of Conceptual Physics is available in PDF (encrypted) format, ensuring compatibility with popular e-readers and mobile devices. The True PDF version offers high-quality typography and graphics, making it ideal for tablets and laptops. Additionally, the book can be accessed via online platforms, allowing readers to study without downloading. The encrypted PDF format protects the content while maintaining readability across multiple devices, including Kindle and Google Play Books. This versatility ensures students can access the material anywhere, anytime.

5.2 Platforms for Online Reading

The 13th Edition of Conceptual Physics can be accessed on various online platforms, allowing readers to study directly in a web browser without downloading. Platforms like Google Play Books and Amazon Kindle support the PDF format, enabling seamless reading on smartphones, tablets, and computers. Additionally, services like Scribd and VitalSource offer online access, making it convenient for students to engage with the material wherever they are. The ISBN-13: 978-1-292-43733-0 ensures easy access to the digital version across these platforms.

ISBN and Edition Details

The 13th Edition of Conceptual Physics by Paul G. Hewitt has an ISBN-13: 978-1-292-43733-0 and ISBN-10: 1-292-43733-2, published as a Global Edition by Pearson in 2023.

6.1 ISBN Numbers for Reference

The 13th Edition of Conceptual Physics by Paul G. Hewitt is identified by specific ISBN numbers. The ISBN-13 is 978-1-292-43733-0, while the ISBN-10 is 1-292-43733-2. These numbers are essential for accurate referencing and purchasing the correct edition. Published by Pearson, the Global Edition ensures accessibility for international students and educators. These ISBNs also help in verifying the authenticity of the book, whether in paperback or digital formats like PDF. Always cross-check ISBNs to avoid purchasing incorrect or unauthorized versions of the textbook.

6.2 Edition-Specific Updates

The 13th Edition of Conceptual Physics includes updated content and applications to enhance student engagement. It features new Hewitt-Drew-It screencasts, which simplify complex concepts through visuals and storytelling. The edition also incorporates modern physics topics, such as quantum mechanics and cosmology, to reflect current scientific understanding. Additionally, the Global Edition ensures relevance to international students by adapting examples and references. These updates make the textbook more accessible and aligned with contemporary educational needs, while maintaining its hallmark of making physics delightful and understandable for learners worldwide.

The 13th Edition of Conceptual Physics is a trusted resource, offering engaging content and updated resources. Ideal for students seeking a clear understanding of physics concepts.

7.1 Final Thoughts on the 13th Edition

The 13th Edition of Conceptual Physics stands out as a comprehensive and engaging resource. Its updated content, including Hewitt-Drew-It screencasts and real-world applications, enhances learning. Students benefit from clear explanations and interactive tools, making complex concepts accessible. The inclusion of a global edition ensures a broad perspective, catering to diverse educational needs. With its balanced approach between theory and practical insights, this edition remains a valuable choice for both students and educators. It continues to set a high standard for physics education.